Pengertian Median, Jenis, Cara Menghitung, Kelebihan, dan Kekurangannya
A. Pengertian Median
Median atau nilai tengah adalah salah satu ukuran pemusatan data, yaitu jika segugus data diurutkan dari yang terkecil sampai yang terbesar atau yang terbesar sampai yang terkecil, nilai pengamatan yang tepat di tengah-tengah bila jumlah datanya ganjil, atau rata-rata kedua pengamatan yang di tengah bila banyaknya pengamatan genap.
Median bisa membantu kita untuk menghitung jumlah data yang relatif kecil. Tetapi nilai median tidak stabil untuk data yang memiliki populasi sama. Median dihitung secara matematis dengan dilambangkan Me. Median membagi dua data berdasarkan urutan nilai.
B. Jenis Median
1. Median Data Tunggal
Median data tunggal yaitu nilai tengah yang dicari dan didapatkan dari penyajin data tunggal. Misalkan 3, 4, 5, 6, 7, 8, 9. Karena 6 berada di tengah maka nilai median dari baris angka tersebut adalah 6. Dalam mencari median data tunggal tentu caranya lebih mudah, karena patokannya adalah hanya pada jumlah data tunggal tersebut. Tetapi jika data yang disajikan jumlahnya genap, diambil 2 data yang berada pada tengah-tengah urutan, lalu dibagi dua. Dengan begitu maka median data tunggal yang jumlah datanya genap bisa diketahui.
2. Median Data Kelompok
Pada penyajian data kelompok biasanya terdapat panjang interval atau jarak dari data satu ke data yang lain. Misalkan 21-25, 26-30, 31-35, 36-40, dan seterusnya. Untuk mengetahui median atau nilai tengah dalam data kelompok kuncinya harus mengetahui frekuensi kumulatif untuk dapat mengolah data. Setelah itu semuanya akan mudah untuk dikerjakan.
C. Cara Menghitung Median
Cara menghitung median bisa dilakukan dengan menyusun data dari yang terkecil hingga yang terbesar.
1. Menghitung Median Data Ganjil
Saat menghitung nilai median dalam data ganjil, langkah pertama yang harus dilakukan adalah menyusun angka terlebih dahulu, yaitu dengan mengumpulkan data dari angka terendah hingga angka terbesar.
Misalnya kumpulan data dengan angka {3, 13, 2, 34, 11, 26, 47}, jika diurutkan akan menjadi angka {2, 3, 11, 13, 26, 34, 47}. Maka nilai median atau angka yang di tengah dalam data ganjil tersebut adalah 13. Karena terdapat tiga angka di kedua sisinya.
Contoh lain
Tentukan median dari data tunggal berikut 7, 7, 6, 9, 8, 9, 7, 5, 7, 9, 9, 8, 7, 9, 8.
Jawaban: Urutkan dahulu data tersebut dari terkecil ke terbesar 5, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 9.
Setelah itu langsung dicari nilai tengahnya, nilai yang berada di tengah-tengah dari keseluruhan data. 5, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 9, 9. Jadi mediannya adalah 8.
2. Menghitung Median Data Genap
Cara menghitung median dalam data genap, bisa dengan membuat daftar angka genap, lalu tentukan pasangan tengah dengan menjumlahkan dan membagi menjadi dua. Misalnya dari kumpulan data {3, 13, 2, 34, 11, 17, 27, 47}, jika diurutkan akan menjadi {2, 3, 11, 13, 17, 27, 34, 47}. Nilai tengah dari kumpulan data tersebut adalah 13 dan 17. Untuk menentukan median dari data tersebut, gunakan cara perhitungan (13+17) : 2 = 15 sehingga nilai mediannya adalah 15.
Contoh lain
Tentukan median dari data tunggal berikut 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9
Jawaban: Setelah diurutkan maka menjadi 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 9, 9, 9, 9
Nah caranya ialah 8 + 8 = 16
Kemudian 16 ÷ 2 = 8
Jadi mediannya adalah 8
3. Menghitung Median Data Kelompok
Median data kelompok bisa dicari apabila telah mengetahui kelas mediannya. Caranya yaitu carilah kelas data yang memuat nilai tengah. Dalam mengolah median data kelompok poin yang harus dicari meliputi tepi bawah kelas median, banyaknya data, frekuensi kumulatif sebelum kelas median, frekuensi kelas median, dan panjang kelas.
Contoh
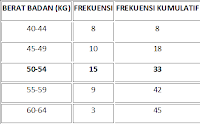
Tentukan median dari data berat badan siswa kelas XII IPS di bawah ini!
 |
| Median Data Kelompok |
Langkah pertama adalah tentukan frekuensi kumulatif data, dengan penyajian tabel sebagai berikut:
 |
| Median Data Kelompok |
Jumlah datanya adalah 45, sehingga nilai tengahnya adalah 23, yang terletak pada kelas interval ke-3 (50-54) sehingga ini kita sebut sebagai kelas median.
Selanjutnya bisa kita peroleh data:
Batas bawah kelas median = 49,5
Frekuensi kumulatif sebelum kelas median = 18
Frekuensi kelas median = 15
Panjang kelas = 5
Maka hasil dari pengolahan data tersebut memperoleh median = 51
D. Kelebihan dan Kekurangan Median
1. Kelebihan, kelebihan dari median adalah terletak pada kemudahan untuk dihitung jika jumlah data relatif kecil dan median sama sekali tidak dipengaruhi oleh nilai pencilan. 2. Kekurangan, kekurangan dari median adalah nilai median relatif tidak stabil bahkan untuk data dalam populasi yang sama.
Dari berbagai sumber

Post a Comment